NeuroBit | @pauloroberto.dev

Parte 2 | Modelos preditivos (capítulos 4 a 10)

Introdução aos modelos preditivos ^[1]

"Um algoritmo de AM preditivo é uma função que, dado um conjunto de exemplos rotulados, constrói um estimador. O rótulo ou etiqueta toma valores em um domínio conhecido. Se esse domínio for um conjunto de valores nominais, tem-se um problema de classificação, também conhecido como aprendizado de conceitos, e o estimador gerado é um classificador. Se o domínio for um conjunto infinito e ordenado de valores, tem-se um problema de regressão, que induz um regressor. Um classificador (ou regressor), por sua vez, também é uma função, que, dado um exemplo não rotulado, atribui esse exemplo a uma das possíveis classes (ou a um valor real) (Dietterich, 1998). Uma definição formal seria, dado um conjunto de observações de pares $D = {(x_{i}, f (x_{i})), i = 1, \dots, n}$ , em que $f$ representa uma função desconhecida, um algoritmo de AM preditivo aprende uma aproximação $\hat{f}$ da função desconhecida $f$ . Essa função aproximada, $\hat{f}$ , permite estimar o valor de $f$ para novas observações de $x$ ." (FACELI et al., 2023, p. 50).

Noutras palavras, consiste em uma função^[2] que mapeia dois conjuntos de dados, sendo um de exemplos rotulados (atributos preditivos/entrada/inputs/variáveis independentes) e outro contendo os rótulos correspondentes - que compõem os dados de treinamento -, com o objetivo de induzir um modelo preditor: um algoritmo que, por aproximação, aprenda a prever o valor que deve ser assumido por outro novo exemplo, não visto anteriormente (alvos/saída/outputs/variáveis dependentes).

Portanto, implementam regras de aprendizagem inerentes ao paradigma supervisionado para a indução do modelo.

Os casos de uso dos modelos preditivos distinguem-se quanto à natureza do que se propõem a resolver, que no mais das vezes são problemas de classificação, em que normalmente se busca categorizar atributos qualitativos de conjuntos com valores finitos (nominais, discretos e não ordenados)^[3], ou regressão, que lida com atributos quantitativos e conjuntos com valores reais infinitos (numéricos, contínuos e ordenados). Respectivamente, o objetivo é "[...] encontrar uma fronteira de decisão que separe os exemplos de uma classe dos exemplos da outra" (FACELI et al., 2023, p. 50) e "[...] aprender uma função que relacione [os objetos] [...]" (FACELI et al., 2023, p. 50).

Para exemplificar, vejamos a imagem a seguir:

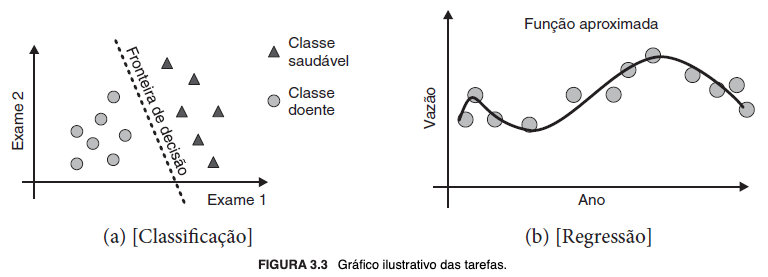
Figura 18 - Gráfico ilustrativo de tarefas (FACELI et al., 2023, p. 50).

Em suma, os problemas de classificação referem-se à tarefa de atribuir um objeto a uma classe, enquanto os de regressão à de prever um valor numérico associado às variáveis independentes (atributos de entrada) a um objeto e que expresse sua relação com os demais. A grosso modo, "em ambos os casos, o objetivo do aprendizado preditivo é aprender uma função $\hat{f} (x)$ , que mapeia as variáveis independentes, os atributos de entrada, na variável objetivo, o atributo alvo." (FACELI et al., 2023, p. 51).

4. Métodos baseados em distâncias

4.1 Considerações gerais e algoritmos dos vizinhos mais próximos

A proximidade entre as variáveis é o aspecto mais relevante, pois "a hipótese base é que dados similares tendem a estar concentrados em uma mesma região no espaço de entrada/características. De maneira alternativa, dados que não são similares estarão distantes entre si." (FACELI et al., 2023, p. 53). A proximidade, que decorre da similitude, é constatada visualmente pelo agrupamento dos pontos na representação gráfica dos dados, que revela áreas com maior densidade de observações.

A premissa fundamental é de que "objetos relacionados com o mesmo conceito são semelhantes entre si" (FACELI et al., 2023, p. 54) — ou, na mesma linha intelectiva, "objetos com características semelhantes pertencem ao mesmo grupo" (FACELI et al., 2023, p. 57) — circunstância que evidencia que, em problemas de classificação, "[...] a distância entre os objetos está relacionada com a definição de suas classes." (FACELI et al., 2023, p. 53). Logo, nesses casos, infere-se que objetos pertencentes à mesma classe estarão concentrados, isto é, próximos uns dos outros. Todavia, esses algoritmos podem ser empregados tanto tarefas de classificação quanto de regressão.

Os principais são os algoritmos dos vizinhos mais próximos, bastante úteis a despeito do funcionamento simplificado. Eles "[...] classifica[m] um novo objeto com base nos exemplos do conjunto de treinamento que são próximos a ele[s] [no espaço de entrada/características]" (FACELI et al., 2023, p. 54) e são considerados algoritmos baseados em memória ou preguiçosos (lazy) porque, na etapa de treinamento, não aprendem diretamente um modelo, mas armazenam ("memorizam") o conjunto de dados de treino - os próprios objetos - para calcular as distâncias e, daí, realizar as predições. Por esse motivo, conclui-se que podem se tornar computacionalmente caros se utilizados com conjuntos muito grandes de dados.

Em sua versão mais simples - algoritmo do 1-Vizinho Mais Próximo (1-Nearest Neighbor - 1-NN) -, cada objeto constitui um ponto no espaço de entrada/características, tal que possibilite calcular o quanto distam entre si por alguma métrica, que usualmente é a distância euclidiana. Nesse caso, a superfície de decisão formará tantos poliedros quantos forem os objetos do conjunto de treinamento, os quais delimitarão a classe de cada objeto. Se os atributos forem qualitativos, pode ser necessário primeiramente convertê-los em valores numéricos. Além disso, se em escalas diferentes, a normalização pode ser necessária.

Por derivação lógica, tem-se o algoritmo K-NN (K-Nearest Neighbors), em que K é um parâmetro - número inteiro positivo — que indica a quantidade de vizinhos a serem considerados. A posição do novo objeto na superfície de decisão é estimada pela agregação dos rótulos dos K vizinhos mais próximos, que corresponde à moda em problemas de classificação e, em problemas de regressão, à média ou à mediana, conforme a função de custo adotada. Dentre as possíveis estratégias para a escolha do valor de K, destacam-se a estimativa por validação cruzada e a ponderação do impacto de cada vizinho em razão inversamente proporcional à distância em relação ao novo objeto.

Esses algoritmos são sensíveis a ruídos, atributos redundantes ou irrelevantes, assim como ao incremento da dimensionalidade do conjunto de dados: tornam-se claramente ineficientes porque, em regra, precisam calcular as distâncias do novo objeto em relação a cada exemplo do conjunto de treinamento memorizado, o que implica no aumento linear da complexidade de tempo desses algoritmos (O(n)). Estratégias como a criação de subconjuntos para atenuar ruídos ou excluir dados redundantes, desde que mantida a representatividade dos exemplos, podem ser utilizadas para contornar a ineficiência computacional. Há também algoritmos especialmente desenvolvidos para identificar no conjunto de treinamento os exemplos mais relevantes. Ademais, destaca-se a estrutura de árvores de busca binária multidimensionais (k-dimensional trees - kd-trees), que "[...] particiona[m] um espaço de busca k-dimensional utilizando os k eixos do sistema de coordenadas [...] definindo, recursivamente, o particionamento do espaço dos dados em subespaços disjuntos." (FACELI et al., 2023, p. 59).

A seguir, representações gráficas simplificadas:

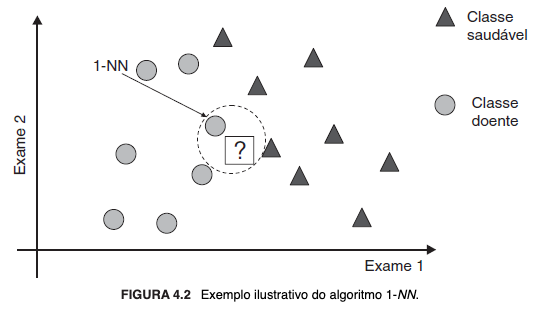
Algoritmo 1-NN — Figura 19 - Gráfico ilustrativo do algoritmo 1-NN (FACELI et al., 2023, p. 55).

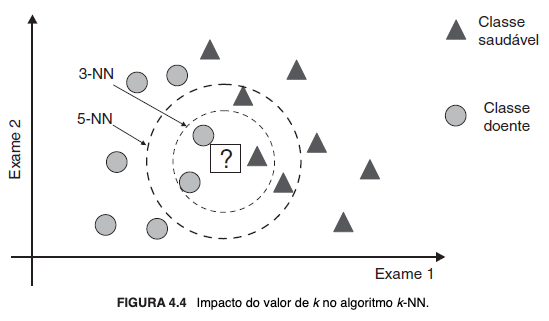
Algoritmo K-NN — Figura 20 - Gráfico ilustrativo do algoritmo K-NN (FACELI et al., 2023, p. 56).

4.2 Raciocínio Baseado em Casos (RBC)

É uma metodologia de resolução de problemas apoiada no aproveitamento do conhecimento adquirido em ocasiões anteriores e como elas foram enfrentadas, no intuito de reaproveitar a experiência acumulada. Envolve a implementação de uma memória ou base de casos para armazenar essas informações, que serão oportunamente recuperadas, readequadas - se necessário - e reaplicadas a outros exemplos. É um método de aprendizado baseado em distância porque, assim como os algoritmos dos vizinhos mais próximos, aproveitam-se da similaridade - ou seja, da proximidade - de casos pretéritos para propor a solução de novos problemas. Diferentemente de outros métodos, não "[...] utilizam o conhecimento geral do domínio ou constroem relações entre problemas e soluções [...]" (FACELI et al., 2023, p. 60), mas focam no enfrentamento através de estratégias específicas, já conhecidas e sabidamente eficazes. Isso permite a constante atualização da base de conhecimento, que será alimentada a cada novo caso resolvido, e induz o aprendizado contínuo e incremental.

Consoante proposto por Aamodt e Plaza (1994), o ciclo do RBC é composto pelas etapas de recuperação, reutilização, revisão e retenção.

Principais tópicos

Modelo preditivo
- É uma função aproximada que relaciona cada elemento de um conjunto rotulado de dados de entrada a um único elemento de um conjunto de rótulos, por conseguinte aprendendo a, por aproximação, rotular novas observações. Essa função aproximada é o próprio resultado do algoritmo de aprendizado de máquina preditivo, induzido pelos dados de treinamento.
- Aprendizagem supervisionada
- Tarefas
  - Classificação: atribuir um objeto a uma classe
  - Regressão: prever um valor numérico que permita extrair a relação entre os atributos de entrada e o atributo alvo
- Métodos baseados em distâncias
  - Dados similares tendem a estar próximos uns dos outros no espaço de entrada/características
  - Algoritmos dos vizinhos mais próximos (1-NN / K-NN)
    - Estimam a posição de um novo objeto no espaço de características com base no exemplo do conjunto de treinamento mais próximo ou nos K exemplos mais próximos a ele, respectivamente.
    - Baseados em memória ou preguiçosos (lazy)
    - Lineares (complexidade de tempo O(n))
  - Raciocínio Baseado em Casos
    - Metodologia de AM que se propõe a resolver problemas com base na experiência acumulada em casos anteriores, a partir da recuperação, reutilização, revisão e retenção de informações em uma memória ou base de casos.
    - O reaproveitamento de conhecimento específico, readequado se necessário, permite a constante atualização da base de conhecimento e o aprendizado incremental.

[ 🔝 ]

Referências complementares

GUIDORIZZI, Hamilton Luiz. Um curso de cálculo, vol. 1. 5. ed. Rio de Janeiro: LTC, 2013.

Notas

[1] Na seção 3.3, os autores distinguem essas abordagens. No entanto, optei por não incluir esses pontos neste momento, uma vez que pretendo estudá-los mais adiante em livros de Estatística. [ 🔙 ]

[2] "Entendemos por uma função $f$ uma terna $(A, B, a \mapsto b)$ , em que $A$ e $B$ são dois conjuntos e $a \mapsto b$ , uma regra que nos permite associar a cada elemento $a$ de $A$ um único $b$ de $B$ . O conjunto $A$ é o domínio de $f$ e indica-se por $D_{f}$ , assim $A = D_{f}$ . O conjunto $B$ é o contradomínio de $f$ . O único $b$ de $B$ associado ao elemento $a$ de $A$ é indicado por $f (a)$ (leia: $f$ de $a$ ); diremos que $f (a)$ é o valor que $f$ assume em $a$ ou que $f (a)$ é o valor que $f$ associa a $a$ ." (GUIDORIZZI, 2013, p. 65). [ 🔙 ]

[3] "Na literatura de AM é usual distinguir modelos generativos de modelos discriminativos. Modelos preditivos discriminativos são aqueles que aprendem uma fronteira de decisão. Modelos generativos, por outro lado, aprendem um modelo para cada classe." (FACELI et al., 2023, p. 52). [ 🔙 ]